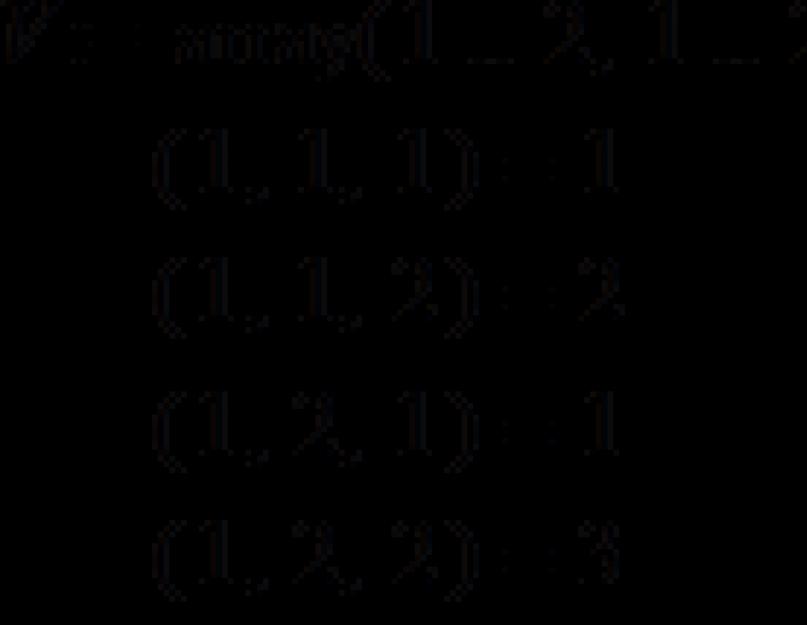Maple как работать на нескольких страницах одновременно. Решение математических задач в Maple

РЕШЕНИЕ МАТЕМАТИЧЕСКИХ ЗАДАЧ

В MAPLE

ЧАСТЬ I

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение высшего

«Нижегородский государственный университет им. »

МАТЕМАТИЧЕСКИХ ЗАДАЧ В MAPLE

факультета для студентов, обучающихся по

направлению подготовки 010100 - «Математика».

Нижний Новгород

УДК 621.396.218

Решение задач в MAPLE. Часть I. Составители: , : Учебно-методическая разработка. – Н. Новгород: Издательство Нижегородского госуниверситета, 2007. – 35 с.

Рецензенты:

доцент кафедры ЧиФА факультета ВМК,

к. ф.-м. н. ,

доцент кафедры ПиУОС Физического факультета,

Данная разработка представляет собой практическое руководство по изучению возможностей пакета аналитических вычислений Maple . Последовательное изучение тем и выполнение заданий позволит шаг за шагом освоить основные приемы работы в математической системе Maple .

Учебно-методическая разработка предназначена для студентов 2 и 3 курсов механико-математического факультета .

УДК 621.396.218

университет им. , 2007

Системы компьютерной алгебры – это новые технологии в научных исследованиях и образовании. В последние годы получили широкое распространение такие системы общего назначения, как Maple, Mathematica.

Система Maple включена в интегрированную систему Scientific WorkPlace и применяется во многих ведущих университетах мира как в научных исследованиях, так и в учебном процессе. Ядро Maple входит в другие распространенные пакеты, такие как MathCad, MathLab.

Данная разработка позволит начинающему войти в технологию использования системы Maple, получить первые навыки, после чего он сможет уже самостоятельно разобраться в более тонких вопросах использования Maple. Хотелось бы отметить, что эта разработка ни в коей мере не является описанием системы Maple. Она предназначена в первую очередь для обучения студентов-математиков решению основных математических задач при помощи Maple.

1. НАЧАЛЬНЫЕ СВЕДЕНИЯ. ТИПЫ ДАННЫХ

Диалог с системой протекает в стиле «вопрос-ответ». Команда начинается с символа > и заканчивается либо точкой запятой (; ), либо двоеточием (: ). Для выполнения команды необходимо нажать клавишу Enter . Если в конце команды стоит точка с запятой, то на экран будет выведен результат действия команды или сообщение об ошибке. Двоеточие в конце команды означает, что команда будет выполнена, но ее результат на экран не будет выводиться. Символ # используется для ввода текстовых комментариев. Также для ввода текста используется клавиша с символом T на панели инструментов. Для возвращения к вводу команд следует нажать клавишу с символом >. Для вызова результата действия предыдущих команд используются символы %, %% или %%%, соответственно. Команда restart отменяет результат действия всех предыдущих команд.

Переменные в Maple характеризуются именем и типом. Имя переменной в Maple может состоять из букв, цифр и некоторых специальных символов, но обязательно должно начинаться с буквы. Ограничений на длину имени нет. Кроме того, Maple различает строчные и прописные буквы. Для присваивания переменной конкретного значения применяется оператор := . Переменные могут использоваться в математических выражениях и функциях без предварительного определения.

Рассмотрим особенности записи в Maple данных числового, строкового и множественного типов.

Выражение принадлежит к целому типу (integer ), если оно состоит из последовательности цифр, не разделенных никакими знаками. Выражения вида a/b, где a, b – целые числа принадлежат к дробному типу (fraction ). К числам с плавающей точкой (float ) относятся выражения вида a. b, a. и. b. Также числа типа float можно записать в показательной форме a*10^b. Комплексные числа (complex ) в Maple записываются в алгебраической форме: a+I*b, где a, b – вещественные числа.

Строковое выражение типа string - это любая конечная последовательность символов, с обеих сторон заключенная в верхние двойные кавычки. Последовательность символов, взятая в обратные кавычки, считается символом (symbol ).

Множество (set ) в Maple задается перечислением в фигурных скобках элементов множества. Например,

> A:={x^n$n=1..6};

> B:={a, a,b, b,b, c};

https://pandia.ru/text/78/155/images/image003_72.gif" width="197" height="26">

Для создания массива используется команда array(i1..j1, i2..j2,..., M), которая возвращает массив с элементами из списка M.

Обращение к элементам множества, списка, массива происходит с указанием индексов элемента в квадратных скобках.

> V:=array(1..2,1..2,1..2,[[,],[,]]);

https://pandia.ru/text/78/155/images/image006_53.gif" width="16 height=19" height="19">

Массив также можно задать командой вида V:=array(1..2,1..2,1..2,); , переопределив затем значения V с помощью оператора присваивания.

В Maple можно записать буквы греческого алфавита в полиграфическом виде. Для этого в командной строке набирается название греческой буквы.

> beta+Gamma+delta;

Задание 1.1

1. Задайте множество A, состоящее из целых чисел от 3 до 20, и множество B, состоящее из квадратов этих чисел. Найдите объединение, пересечение, разность множеств A и B. Найдите мощности всех полученных множеств.

2. Задайте произвольный список и четырехмерный массив.

2. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ, ФУНКЦИИ. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ

ВЫРАЖЕНИЙ И РЕШЕНИЕ УРАВНЕНИЙ

2.1. Вычисления в Maple

Для записи математических выражений в Maple используются операторы сложения (+), вычитания (-), умножения (*), деления (/), возведения в степень (^), оператор присваивания (:=). Порядок выполнения математических операций является стандартным.

Пример.

> (a*b^4-(a*b)^4)/7;

Основные константы в Maple обозначаются следующим образом: Pi - число π, I - мнимая единица i, exp(1) - основание натуральных логарифмов e, infinity – бесконечность, true - истина, false – ложь. Используются следующие знаки сравнения: <, >, >=,<=, <>, = .

Система Maple одинаково успешно справляется как с символьными вычислениями, так и с численными. По умолчанию расчеты проводятся символьно.

Пример.

>1/2+123/100+ sqrt (3);

Часть выражения, в которой встречается число, записанное с плавающей запятой (float), будет вычислена приближенно.

Пример.

>2+ sqrt (2.0)- Pi ;

Все вычисления по умолчанию проводятся с десятью значащими цифрами. Количество значащих цифр можно изменить, применив команду > Digits : = n .

Для того, чтобы получить значение выражения в численном виде используется функция

https://pandia.ru/text/78/155/images/image012_43.gif" width="414" height="19">

2.2. Задание функций

В Maple встроено большое количество функций. Перечислим обозначения для основных элементарных функций..gif" width="83 height=57" height="57">

Рассмотрим несколько способов определения новых функций:

1) присваивание переменной некоторого выражения

имя переменной:=выражение;

имя переменной(список параметров):=выражение;

Пример.

> f (t ):= cos (t )^2+1;

> f (0);

При таком способе задания функции для того, чтобы вычислить значение функции в некоторой точке нужно определить с помощью оператора присваивания значения переменных (параметров), либо использовать оператор подстановки subs.

https://pandia.ru/text/78/155/images/image018_28.gif" width="106" height="33">

> value(%);

https://pandia.ru/text/78/155/images/image021_25.gif" width="100" height="33">

>x := Pi : y :=10: f ;

Команда value (выражение) используется для вычисления значения выражения.

Следует обратить внимание на то, что после присвоения переменной x конкретного значения x:=a, переменная x перестанет быть неопределенной. Вернуть x статус непределенной переменной можно командой > x := evaln (x ); или снять присваивание командой > x :=’ x ’ ; либо отменить все присваивания командой restart .

2) Определение функции с помощью функционального оператора

имя функции:=список параметров -> выражение;

Обращение к функции, заданной таким способом, происходит стандартным образом: имя функции(a, b, …), где a, b, … - конкретные значения переменных.

Пример.

> f 1:=(x , y , z ) -> x ^(y ^ z );

> f1(2,2,2); f1(x,2,2);

https://pandia.ru/text/78/155/images/image024_25.gif" width="25" height="26 src=">

3) Функцию можно задать с помощью команды

unapply(выражение, параметры) , которая преобразовывает выражение в функциональный оператор.

Пример.

> f2:=unapply(sin(x)^2+2*exp(y^2),x, y);

> f 2(Pi /4,1);

https://pandia.ru/text/78/155/images/image027_22.gif" width="189" height="107"> используется команда

https://pandia.ru/text/78/155/images/image028_21.gif" width="248" height="77">

> f1:=convert(f, piecewise);

> f2:=unapply(f1,x);

> f 2(-1/2); f 2(-1);

https://pandia.ru/text/78/155/images/image032_20.gif" width="196" height="27">.gif" width="73" height="49">. Упростите полученные выражения.

3. Найдите значение выражения . Для выполнения преобразований комплексного числа применяется функция evalc .

4. Запишите функцию без знака модуля.

5. Задайте и найдите f(-10)+3f(-1)+f(3).

6. Задайте функцию в виде функционального оператора и найдите ее значение при x=-1, y=.

2.3. Преобразование математических выражений

Maple обладает широкими возможностями для аналитических преобразований математических формул. К ним относятся такие операции, как приведение подобных, разложение на множители, раскрытие скобок, приведение рациональной дроби к нормальному виду и многие другие.

В Maple можно преобразовывать как все выражение в целом, так и отдельные его части.

Для выделения левой (правой) части в математическом выражении вида A=B используются команды

lhs (выражение);

rhs (выражение);

Для выделения числителя (знаменателя) используются команды

numer (выражение);

denom (выражение);

Пример .

>F:=(a^3+b)/(a-b)=3*a^2+b^2/(a+b);

>numer(rhs(F));

>denom (rhs (F ));

Для выделения некоторой части выражения, списка или множества служит команда

op (i ,выражение) , где i – число, определяющее позицию в выражении.

Пример.

> x + y + z ; >op (2,%);

Gif" width="12" height="12 src="> isolate (уравнение, выражение);

Пример .

> P := 2* ln (x )* exp (x ) -3* exp (y )+7=10* ln (x ) - exp (y ):

> isolate(P, y);

> R:=5*(x^2)*sin(x)+1=5*sin(x):

> isolate (R , sin (x ));

1) Приведение подобных членов в выражении по переменной осуществляется командой

https://pandia.ru/text/78/155/images/image047_14.gif" width="439" height="28">

2) Разложить на множители выражение можно с помощью команды

https://pandia.ru/text/78/155/images/image050_16.gif" width="186" height="56">

>factor(x^4-3*x^3+2*x^2+3*x-9);

>factor(x^3+x-3*sqrt(2));

>factor(x^3+16, {2^(1/3),sqrt(3)});

>alias(w=RootOf(x^3+2*x+1)); factor(x^3+2*x+1,w);

https://pandia.ru/text/78/155/images/image055_15.gif" width="504" height="26 src=">

> convert(%,radical);

https://pandia.ru/text/78/155/images/image057_17.gif" width="303" height="57">

> factor(x^2+x+1,complex);

Gif" width="12" height="12 src="> expand (выражение, опции) , где в опциях можно указать выражение, скобку с которым раскрывать не следует. Данную команду также используют для действий с экспонентами и сведения тригонометрических выражений к тригонометрическим функциям простых аргументов.

Пример .

>expand((x+1)*(x+2)*(x+3)*(x+4));

>expand((x+y)*(x+3), x+3);

>expand(exp(a-n*b+ln(c)));

>expand (tan (3* x ));

4) Привести дробь к нормальному виду можно с помощью команды

https://pandia.ru/text/78/155/images/image063_16.gif" width="60" height="54">

>normal(sin(2*x+3+4/(x-1)+5/(x-2)), expanded);

5) Для преобразований выражений, содержащих радикалы, применяется команда

rationalized " для того, чтобы избавиться от иррациональностей в знаменателях, " expanded " для раскрытия всех скобок.

Пример .

> (7+5* sqrt (2))^(1/3);

> radnormal ((7+5* sqrt (2))^(1/3));

> a := sqrt (3)/(3^(1/2)+6^(1/2));

rationalized ");

6) Упрощение выражений осуществляется командой

DIV_ADBLOCK515">

Пример .

>(sqrt(2)+sqrt(3))*(sqrt(2)-sqrt(3));

>simplify((sqrt(2)+sqrt(3))*(sqrt(2)-sqrt(3)));

> f:=(1-cos(x)^2+sin(x)*cos(x))/(sin(x)*cos(x)+cos(x)^2); simplify(f, trig);

Также в опциях указываются предположения о значении аргумента. Для формальных символьных преобразований многозначных функций в опциях можно указать symbolic .

Пример .

> g:=sqrt(x^2);

> simplify(g, assume=real);

> simplify(g, assume=positive);

>simplify(g, symbolic);

Команда simplify позволяет выполнить преобразования в выражении при заданных условиях (условия указываются в фигурных скобках).

Пример .

> f:= -3*x*y + x+y: simplify(f, {x = a-b, y = a+b});

В некоторых случаях бывает полезно предварительно преобразовать выражение при помощи команды

https://pandia.ru/text/78/155/images/image076_12.gif" width="276" height="54">

>simplify(B, trig);

>convert(%,tan):

>simplify (%);

7) Объединить части выражения по определенным правилам можно при помощи команды

https://pandia.ru/text/78/155/images/image079_12.gif" width="94" height="25 src=">, , при указании опции ln происходит потенцирование. Так же как для simplify в опциях можно указать symbolic .

Пример .

> combine(exp(sin(a)*cos(b))*exp(-cos(a)*sin(b)),);

>combine((a^3)^2+a^3*a^3);

Gif" width="12" height="12 src="> solve(уравнение, переменные).

Переменные перечисляются в фигурных скобках через запятую. Если не указывать набор переменных в параметрах команды, то решение будет найдено для всех переменных, участвующих в уравнениях. Если требуется решить систему уравнений, то уравнения системы указываются в фигурных скобках через запятую. Результатом применения команды solve будет список решений данного уравнения, либо, если уравнение не имеет решений или командой solve они не могут быть найдены, в строке вывода не появится никаких сообщений. Со списком решений можно работать так же как с обычным списком.

Пример .

> eq:=(x-1)^3*(x-2)^2;

> s:=solve(eq);

> solve(x^4-11*x^3+37*x^2-73*x+70);

https://pandia.ru/text/78/155/images/image086_12.gif" width="349" height="22 src=">

>e:=solve(AX);

>rhs(e); subs(e, z);

DIV_ADBLOCK517">

Пример.

>e1:={x^2-y^2=1,x^2+x*y=3};

> s:=solve(e1,{x, y});

> _EnvExplicit:=true:

> solve(e1,{x, y});

Максимальное количество решений, которое может быть найдено с помощью команды solve, определяется значением глобальной переменной _MaxSols , имеющей по умолчанию значение равное 100. Если придать глобальной перменной _EnvAllSolutions значение true , то в случае бесконечного множества решений, команда solve для некоторых уравнений сможет оформить ответ в виде выражения, содержащего переменные определенного типа. Например, для тригонометрических уравнений ответ будет содержать целочисленные параметры вида _Z~.

Пример.

> _EnvAllSolutions:= true:

>solve(sin(2*x)=cos(x), x);

https://pandia.ru/text/78/155/images/image094_11.gif" width="274" height="51 src=">.gif" width="12" height="12 src="> f solve(уравнение, переменные, опции).

В опциях можно указать интервал, в котором будет производиться поиск корней, также можно указать complex - для нахождения всех комплексных корней, либо опцию maxsols=n – для нахождения n наименьших корней полинома. Если уравнение задано полиномом, то команда fsolve будет находить все вещественные приближенные корни, в общем случае команда fsolve будет находить только один численный корень уравнения, другие корни можно искать, изменяя интервал поиска так, чтобы найденный корень в него не входил.

Пример .

> fsolve(x-cos(x));

https://pandia.ru/text/78/155/images/image097_10.gif" width="641" height="23">

Для разрешения реккурентностей применяется команда

https://pandia.ru/text/78/155/images/image098_10.gif" width="255" height="22 src=">

> rsolve(e1,f);

> rsolve({e1,f(0)=1,f(1)=2},f);

С помощью команды solve также можно решать неравенства и системы уравнений и неравенств.

Пример .

> solve(ln(x)<1, x);

https://pandia.ru/text/78/155/images/image102_8.gif" width="119" height="23 src=">

> solve({x-y>=1,x-2*y<=1,x-3*y=0,x+y>=1},{x, y});

https://pandia.ru/text/78/155/images/image104_7.gif" width="180" height="56">.

2. Упростите выражение .

3. Упростите выражение .

4.Приведите подобные в выражении и вычислите его значение при a=-3, x=1.

5. Упростите выражение а) ; б) .

6. Избавьтесь от иррациональностей в знаменателе выражения .

7. Выразите , https://pandia.ru/text/78/155/images/image113_7.gif" width="46" height="48 src="> в радикалах.

8. Доказать, что , если A, B, C – углы треугольника.

9. Выразите через и https://pandia.ru/text/78/155/images/image118_7.gif" width="164" height="41">;

б) https://pandia.ru/text/78/155/images/image120_7.gif" width="88" height="47 src=">.

11. Разложите многочлен на множители над полем вещественных чисел и над полем рациональных чисел. Найдите разложение в радикалах.

12. Разложите многочлен на множители над полем вещественных чисел и над полем комплексных чисел. Найдите разложение в радикалах.

13. Решите уравнение .

14. Решите систему уравнений .

15. Решите систему уравнений и упростите ответ.

16. Численно найти все решения уравнения .

17. Найти три численных решения уравнения .

18. Решите систему неравенств .

19. Решите неравенство .

3 . ПОСТРОЕНИЕ ГРАФИКОВ

Эта часть посвящена возможностям системы Maple V в визуализации самых разнообразных вычислений.

3.1. Двумерные графики

Для построения графиков функции f(x) от одной переменной (в интервале https://pandia.ru/text/78/155/images/image132_6.gif" width="69" height="24"> по оси Оу ) используется команда

plot(f(x), x=a..b, y=c..d, options),

где options – опция или набор опций, задающих стиль построения графика. Если их не указывать, то будут использованы установки по умолчанию. Настройка изображения также может осуществляться с панели инструментов. Для этого следует щелкнуть левой кнопкой мыши по изображению. После этого становятся активными кнопки в нижнем ряду панели. Также можно узнать координаты точки на графике. Для этого необходимо подвести курсор к нужной точке графика и щелкнуть левой кнопкой мыши. Слева в нижнем ряду кнопок на панели появятся координаты. Настройка изображения также может осуществляться с помощью контекстного меню. Оно вызывается правой кнопкой мыши.

Основные параметры команды plot :

title=”text”, где text- заголовок рисунка (текст можно оставлять без кавычек, если он не содержит пробелов).

coords=polar – установка полярных координат (по умолчанию установлены декартовы).

axes – установка типа координатных осей: axes=NORMAL – обычные оси; axes=BOXED – график в рамке со шкалой; axes=FRAME – оси с центром в левом нижнем углу рисунка; axes=NONE – без осей.

scaling – установка масштаба рисунка: scaling=CONSTRAINED – одинаковый масштаб по осям; scaling=UNCONSTRAINED – график масштабируется по размерам окна.

style = LINE – вывод линиями, style = POINT вывод точками.

numpoints=n – число вычисляемых точек графика (по умолчанию n=50 ).

сolor – установка цвета линии: английское название цвета, например, yellow – желтый и т. д.

xtickmarks=nx и ytickmarks=ny – число меток по оси Оx и оси Оy , соответственно.

thickness=n, где n=1,2,3… - толщина линии (по умолчанию n=1 ).

linestyle=n – тип линии: непрерывная, пунктирная и т. д. (по умолчанию n=1 – непрерывная).

symbol=s - тип символа, которым помечают точки: BOX, CROSS, CIRCLE, POINT, DIAMOND .

font= – установка типа шрифта для вывода текста: f задает название шрифтов: TIMES, COURIER, HELVETICA, SYMBOL; style задает стиль шрифта: BOLD, ITALIC, UNDERLINE; size – размер шрифта в pt.

labels= – надписи по осям координат: tx – по оси Оx и ty – по оси Оy .

discont=true – указание для построения бесконечных разрывов, при этом на графике асимптоты не рисуются.

Пример. Построить график https://pandia.ru/text/78/155/images/image134_1.jpg" width="292 height=292" height="292">

Построение графика функции, заданной параметрически

С помощью команды plot можно строить также графики функций, заданных параметрически y=y(t), x=x(t) :

plot(, parameters) .

Пример. Построить график параметрической кривой , https://pandia.ru/text/78/155/images/image138_2.jpg" width="231 height=164" height="164">

Построение графика функции, заданной неявно

Для построения графика неявной функции F(x, y)=0 используется команда https://pandia.ru/text/78/155/images/image139_5.gif" width="80" height="27">.

>with(plots):implicitplot(x^2+y^2=1, x=-1..1, y=-1..1);

Gif" width="12 height=12" height="12"> textplot(, options), где x0, y0 – координаты точки, с которой начинается вывод текста ’text’ .

Вывод нескольких графических объектов на один рисунок

Если на одном рисунке нужно совместить несколько графиков функций, то можно воспользоваться командой

plot({f1(x), f2(x), …}, options);

Если необходимо нарисовать несколько графических объектов, полученных при помощи различных команд, то для этого результат действия команд присваивается некоторым переменным:

> p := plot (…): t := textplot (…):

При этом на экран вывод не производится. Для вывода графических изображений необходимо выполнить команду из пакета plots:

display(, options) .

Пример . Построить графики функций https://pandia.ru/text/78/155/images/image142_6.gif" width="73" height="20 src=">.gif" width="59" height="24 src="> на одном рисунке.

> with(plots):

> p1:=plot(sin(x), x=-5..5, y=-2..2, thickness=3, color=blue):

> p2:=plot(cos(x), x=-5..5, y=-2..2, thickness=3, color=green):

> p3:=plot(tan(x), x=-5..5, y=-2..2, thickness=3, color=black):

> p4:=plot(ln(x), x=-5..5, y=-2..2, thickness=3, color=red):

> display(p1,p2,p3,p4);

https://pandia.ru/text/78/155/images/image146_5.gif" width="297 height=24" height="24"> , то для этого можно использовать команду inequal из пакета plots:

inequals({f1(x, y)>c1,…,fn(x, y)>cn}, x=x1…x2, y=y1..y2, options)

В фигурных скобках указывается система неравенств, задающих область, затем размеры координатных осей и параметры. С помощью параметров можно регулировать толщину линий границ, цвета открытых и закрытых границ, цвета внешней и внутренней областей:

.gif" width="12" height="12 src=">optionsexcluded=(color=yellow) – установка цвета внешней области;

.gif" width="12" height="12 src=">optionsclosed(color=green, thickness=3) – установка цвета и толщины линии закрытой границы.

Задание 3.1

1. Построить график https://pandia.ru/text/78/155/images/image148_6.gif" width="75" height="43">.

3..gif" width="72" height="20">, в рамке.

4..gif" width="83" height="23 src=">

> plot(1-sin(x^2), x=0..2*Pi, coords=polar, color=black, thickness=4);

5. Построить график гиперболы: .

6..gif" width="75" height="20 src=">) вписанной в эллипс . Подпишите эти линии жирным шрифтом курсивом.

> with (plots ):

> eq := x ^2/16+ y ^2/4=1:

> el:=implicitplot(eq, x=-4..4, y=-2..2, scaling=CONSTRAINED, color=green, thickness=3):

> as:=plot(, color=blue, scaling=CONSTRAINED, thickness=2):

> eq1:=convert(eq, string):

> t1:=textplot(, font=, align=RIGHT):

> t2:=textplot(, font=, align=RIGHT):

> t3:=textplot(, font=, align=LEFT):

> display();

7. Построить область, ограниченную линиями: , , .

> with (plots ):

> inequal({x+y>0, x-y<=1, y=2}, x=-3..3, y=-3..3,

optionsfeasible=(color=red),

optionsopen=(color=blue, thickness=2),

optionsclosed=(color=green, thickness=3),

optionsexcluded=(color=yellow));

3 .2. Трехмерные графики. Анимация

График поверхности, заданной явной функцией

График функции можно построить, используя команду

plot3d(f(x, y), x=x1…x2, y=y1…y2, options) .

Параметры этой команды частично совпадают с параметрами команды plot. К часто используемым параметрам команды plot3d также относится

light= – задание подсветки поверхности, создаваемой из точки со сферическими координатами (angl1 , angl2 ). Цвет определяется долями красного (c1 ), зеленого (c2 ) и синего (c3 ) цветов, которые находятся в интервале .

style=opt задает стиль рисунка: POINT –точки, LINE – линии, HIDDEN – сетка с удалением невидимых линий, PATCH – заполнитель (установлен по умолчанию), WIREFRAME – сетка с выводом невидимых линий, CONTOUR – линии уровня, PATCHCONTOUR – заполнитель и линии уровня.

shading=opt задает функцию интенсивности заполнителя, его значение равно xyz – по умолчанию, NONE – без раскраски.

Трехмерные изображения удобнее настраивать не при помощи опций команды plot3d , а используя контекстное меню программы. Для этого следует щелкнуть правой кнопкой мыши по изображению. Тогда появится контекстное меню настройки изображения. Команды этого меню позволяют изменять цвет изображения, режимы подсветки, устанавливать нужный тип осей, тип линий. Так же как и для двумерных графиков можно активировать нижний ряд кнопок на панели инструментов, щелкнув левой кнопкой мыши по изображению. Поворачивать изображение можно с помощью кнопок панели или удерживая левую кнопку мыши.

Пример. Построить поверхность вместе с линиями уровня

https://pandia.ru/text/78/155/images/image160_0.jpg" width="321" height="198">

График поверхности, заданной параметрически

Если требуется построить поверхность, заданную параметрически: x =x (u ,v ), y =y (u ,v ), z =z (u ,v ), то эти функции перечисляются в квадратных скобках в команде:

plot3d(, u=u1..u2, v=v1..v2) .

Пример . Построить тор.

> plot3d(, s=0..2*Pi, t=0..11*Pi/6, grid=, style=patch, axes=frame, scaling=constrained);

https://pandia.ru/text/78/155/images/image162_4.gif" width="99" height="24">, строится с помощью команды пакета plot s :

implicitplot3d(F(x, y,z)=c, x=x1..x2, y=y1..y2, z=z1..z2), где указывается уравнение поверхности и размеры рисунка по координатным осям.

График пространственных кривых

В пакете plot s имеется команда spacecurve для построения пространственной кривой, заданной параметрически: .

spacecurve ([ x (t ), y (t ), z (t )], t = t 1.. t 2) , где переменная t изменяется от t1 до t2 .

Построение нескольких трехмерных фигур на одном графике

Команда plot 3 d позволяет строить одновременно несколько фигур, пересекающихся в пространстве. Для этого достаточно вместо описания одной поверхности задать список описаний ряда поверхностей. При этом функция plot 3 d обладает уникальной возможностью – автоматически вычисляет точки пересечения фигур и показывает только видимые части поверхностей. Это создает изображения, выглядящие вполне естественно.

Пример. Выполнить построение двух поверхностей и в пределах https://pandia.ru/text/78/155/images/image168_4.gif" width="39" height="19">.

> plot 3 d ({ x * sin (2* y )+ y * cos (3* x ), sqrt (x ^2+ y ^2)-7}, x =- Pi .. Pi , y =- Pi .. Pi , grid =, axes = FRAMED , color = x + y );

Анимация

Maple позволяет выводить на экран движущиеся изображения с помощью команд animate (двумерные) и animate3d (трехмерные) из пакета plot s . Суть анимации при использовании данных функций заключается в построении серии кадров, причем каждый кадр связан со значением изменяемой во времени переменной t. Среди параметров команды animate3d есть

frames – число кадров анимации (по умолчанию frames=8 ).

Управлять движущимся изображением удобнее с помощью контекстного меню.

Задание 3 .2

1. Построить график поверхности .

2. Построить шар :

3..gif" width="65" height="21 src=">.gif" width="173 height=53" height="53">.gif" width="95" height="48 src=">.gif" width="71" height="23 src=">.

Выведите название рисунка, подпишите названия осей и установите одинаковый масштаб по осям.

6. Нарисовать движущийся объект – лист Мебиуса.

4 . МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Рассмотрим основные функции для решения задач математического анализа, встроенные в пакет Maple.

4 .1. Предел функции и дифференцирование

Вычисление пределов осуществляется при помощи команды

.gif" width="12" height="12 src=">Limit (выражение, x=a, параметры) .

Пример .

>Limit(ln(cos(a*x))/(ln(cos(b*x))), x=0)=limit(ln(cos(a*x))/(ln(cos(b*x))), x=0);https://pandia.ru/text/78/155/images/image181_4.gif" width="215" height="58 src=">

Дифференцирование в Maple выполняется при помощи команды

DIV_ADBLOCK519">

https://pandia.ru/text/78/155/images/image182_4.gif" width="262" height="54">

Кафедра: Информационные Технологии

Лабораторная Работа

На тему: "СИНТАКСИС, ОСНОВНЫЕ ОБЪЕКТЫ И КОМАНДЫ СИСТЕМЫ MAPLE "

Москва, 2008 год

Цели работы :

· знать основные объекты и переменные системы Maple;

· знать и уметь применять команды, используемые при работе с объектами и переменными системы Maple;

· знать синтаксис основных математических функций системы Maple.

Введение

Система аналитических вычислений Maple – интерактивная система. В данном случае это означает, что пользователь вводит команду или оператор языка Maple в области ввода рабочего листа и, нажав клавишу , сразу же передает ее аналитическому анализатору системы, который выполняет ее. При правильном введении команды в области вывода появляется результат выполнения этой команды, если команда содержит синтаксические ошибки или ошибки выполнения, система печатает сообщение об этом. Если ошибку надо исправить, то следует вернуться к оператору, откорректировать его и снова выполнить. Выполнив введенную команду, система ожидает очередной команды от пользователя. Можно вернуться в любой момент к любой команде или оператору на рабочем листе, подкорректировать его и снова выполнить. Однако, если на рабочем листе есть команда, использующая результат вновь вычисленной, то ее следует также снова вычислить, установив на нее курсор, и, нажав клавишу , а если таких команд много, то можно выполнить команду графического интерфейсаEdit ® Execute ® Worksheet для повторного вычисления всех команд рабочего листа.

Каждый оператор или команда обязательно завершаются разделительным знаком. Таких знаков в системе Maple два – точка с запятой (;) и двоеточие (:). Если предложение завершается точкой с запятой, то оно вычисляется, а в области вывода отображается результат. При использовании двоеточия в качестве разделителя команда выполняется, но результаты ее работы не отображаются в области вывода рабочего листа. Это удобно, например, при программировании в Maple, когда нет необходимости в выводе каких-то промежуточных результатов, получаемых из операторов цикла, так как вывод этих результатов может занять много места на рабочем листе, да и может потребоваться значительное количество времени на их отображение.

Здесь и далее для команд Maple используется запись в форме синтаксиса языка Maple. Если при выполнении примеров возникает желание отображать команды в математической нотации, то следует командой Options ® Input Display ® Standard Math Notation установить соответствующий режим отображения.

В Maple реализован свой язык, с помощью которого происходит общение пользователя с системой. Базовыми понятиями являются объекты и переменные, из которых с помощью допустимых математических операций составляются выражения.

Простейшими объектами , с которыми может работать Maple , являются числа, константы и строки.

Числа

Числа в системе Maple могут быть следующих типов: целые, обыкновенные дроби, радикалы, числа с плавающей точкой и комплексные. Первые три типа чисел позволяют выполнять точные вычисления (без округлений) разнообразных математических выражений, реализуя точную арифметику. Числа с плавающей точкой являются приближенными, в которых число значащих цифр ограничено. Эти числа служат для приближения (или аппроксимации) точных чисел Maple. Комплексные числа могут быть как точными, если действительная и мнимая части представлены точными числами, так и приближенными, если при задании действительной и мнимой частей комплексного числа используются числа с плавающей точкой.

Целые числа задаются в виде последовательности цифр от 0 до 9. Отрицательные числа задаются со знаком минус (–) перед числом, нули перед первой ненулевой цифрой являются не значащими и не влияют на величину целого числа. Система Maple может работать с целыми числами произвольной величины, количество цифр практически ограничено числом 2 28 . Вычисления с целыми числами реализуют четыре арифметических действия (сложение +, вычитание –, умножение *, деление /) и вычисление факториала (!).

Maple представляет большое целое число, которое не помещается в строке области вывода используя символ обратного слэша (\) в качестве символа продолжения вывода на следующей строке. Последняя команда вычисляет количество цифр в результате предыдущего вычисления. В ней в качестве параметра используется операция%, которая является всего лишь удобной формой ссылки на результат выполнения предыдущей операции. В Maple имеются еще две подобные операции, которые идентифицируют результаты предпредыдущей и предпредпредыдущей команд.Их синтаксис выглядит, соответственно, следующим образом:

В Maple имеется достаточно большой набор команд, позволяющих выполнить действия, специфичные при обработке целых чисел: разложение на простые множители (ifactor), вычисление частного (iquo) и остатка (irem) при выполнении операции целого деления, нахождения наибольшего общего делителя двух целых чисел (igcd), выполнение проверки, является ли целое число простым (isprime) и многое другое.

Для проверки вычисления частного и остатка двух целых чисел использованы операции получения результата выполнения предыдущей (вычисление частного) и предпредыдущей (вычисление остатка) команд. Результатом команды isprime () является булева константа true (истина) или false (ложь).

Набрав в области ввода рабочего листа команду? integer, можно получить список всех команд для работы с целыми числами

Обыкновенные дроби задаются с помощью операции деления двух целых чисел. Заметим, что Maple автоматически производит операцию сокращения дробей. Над обыкновенными дробями можно выполнять все основные арифметические операции.

Если при задании дроби ее знаменатель сокращается (см. последнее вычисление в примере), то такая «дробь» трактуется системой Maple как целое число.

Часто представление результата в виде обыкновенной дроби не совсем удобно, и возникает задача преобразования ее в десятичную дробь. Для этого используется команда evalf(), которая аппроксимирует обыкновенную дробь числами с плавающей точкой, используя десять значащих цифр в мантиссе их представления. Если точность по умолчанию не достаточна, то ее можно задать вторым параметром указанной функции.

Дробь и ее десятичное представление не являются идентичными объектами Maple. Десятичное представление всего лишь аппроксимация точной величины, представленной обыкновенной дробью.

Радикалы задаются как результат возведения в дробную степень целых или дробных чисел, или вычисления из них же квадратного корня функцией sqrt(), или вычисления корня n ‑ой степени с помощью функции surd (число, n). Операция возведения в степень задается символом ^ или последовательностью из двух звездочек (**). При возведении в степень дробей их следует заключать в круглые скобки, как, впрочем, и дробный показатель степени. При задании радикалов также производятся возможные упрощения, связанные с вынесением из-под знака радикала максимально возможной величины.

Вычисления с целыми, дробями и радикалами являются абсолютно точными, поскольку при работе с этими типами данных программа Maple не производит никаких округлений в отличие от чисел с плавающей точкой.

Числа с плавающей точкой задаются в виде целой и дробной частей, разделенных десятичной точкой, с предшествующим знаком числа, например, 3.4567, -3.415. Числа с плавающей точкой можно задавать, используя так называемую экспоненциальную форму записи, в которой сразу же после вещественного числа с плавающей точкой или обычного целого, называемого мантиссой, ставится символ е или е, после которого задается целое число со знаком (показатель степени). Такая форма записи означает, что мантиссу следует умножить на десять в степени числа, соответствующего показателю степени, чтобы получить значение числа, записанного в такой экспоненциальной форме. Например, 2.345е4 соответствует числу 23450.0. Таким образом, можно представлять очень большие по абсолютному значению числа (показатель степени положительное число) или очень маленькие (показатель степени отрицательное число).

Из чисел составляются математические выражения с помощью арифметических операций. Символы арифметических операций в Maple перечислены в табл. 1.

Таблица 1. Арифметические операции

Последовательность выполнения арифметических операций соответствует стандартным правилам старшинства операций в математике: сначала производится возведение в степень, затем умножение и деление, а в конце – сложение и вычитание. Все действия выполняются слева направо. Операция вычисления факториала имеет наибольший приоритет. Для изменения последовательности арифметических операций следует использовать круглые скобки.

Если все числа в выражении являются целыми, дробями или радикалами, то результат представляется также с использованием этих типов данных, но если в выражении присутствует число с плавающей точкой, то результатом вычисления такого «смешанного» выражения будет также число с плавающей точкой, если только в выражении не присутствует радикал. В этом случае радикал вычисляется точно, а коэффициент при нем вычисляется либо точно, либо в виде числа с плавающей точкой в зависимости от типа сомножителей.

Система аналитических вычислений Maple всегда пытается произвести вычисления с абсолютной точностью. Если это не получается, тогда подключается арифметика с вещественными числами.

Maple умеет работать и с комплексными числами . Для мнимой единицы

в Maple используется константа I . Задание комплексного числа не отличается от его обычного задания в математике.

В Maple имеется несколько способов представления функции.

Способ 1. Определение функции с помощью оператора присваивания (:= ): какому-то выражению присваивается имя, например:

> f:=sin(x)+cos(x);

Если задать конкретное значение переменной х , то получится значение функции f для этого х . Например, если продолжить предыдущий пример и вычислить значение f при , то следует записать:

> x:=Pi/4;

После выполнения этих команд переменная х имеет заданное значение .

Чтобы насовсем не присваивать переменной конкретного значения, удобнее использовать команду подстановки subs({x1=a1, x2=a2,…, },f), где в фигурных скобках указываются переменные хi и их новые значения аi (i =1,2,…), которые следует подставить в функцию f . Например:

> f:=x*exp(-t);

> subs({x=2,t=1},f);

Все вычисления в Maple по умолчанию производятся символьно, то есть результат будет содержать в явном виде иррациональные константы, такие как, и другие. Чтобы получить приближенное значение в виде числа с плавающей запятой, следует использовать команду evalf(expr,t), где expr – выражение, t – точность, выраженная в числах после запятой. Например, в продолжение предыдущего примера, вычислим полученное значение функции приближенно:

> evalf(%);

Здесь использован символ (% ) для вызова предыдущей команды.

Способ 2. Определение функции с помощью функционального оператора, который ставит в соответствие набору переменных (x1,x2,…) одно или несколько выражений (f1,f2,…) . Например, определение функции двух переменных с помощью функционального оператора выглядит следующим образом:

> f:=(x,y)->sin(x+y);

Обращение к этой функции осуществляется наиболее привычным в математике способом, когда в скобках вместо аргументов функции указываются конкретные значения переменных. В продолжение предыдущего примера вычисляется значение функции:

Способ 3. С помощью команды unapply(expr,x1,x2,…) , где expr – выражение, x1,x2,… – набор переменных, от которых оно зависит, можно преобразовать выражение expr в функциональный оператор. Например:

> f:=unapply(x^2+y^2,x,y);

В Maple имеется возможность определения неэлементарных функций вида

посредством команды

> piecewise(cond_1,f1, cond_2, f2, …).

Например, функция

записывается следующим образом.

В Maple имеется несколько способов представления функции.

> f:=sin(x)+cos(x);

> x:=Pi/4;

После выполнения этих команд переменная х имеет заданное значение .

> f:=x*exp(-t);

> subs({x=2,t=1},f);

> evalf(%);

Здесь использован символ (% ) для вызова предыдущей команды.

> f:=(x,y)->sin(x+y);

> f:=unapply(x^2+y^2,x,y);

В Maple имеется возможность определения неэлементарных функций вида

посредством команды

> piecewise(cond_1,f1, cond_2, f2, …).

Например, функция

записывается следующим образом.

04. 01 Преобразование уравнений. Команды lhs и rhs

* Entering and Manipulating Equations: The lhs and rhs commands *

Напомним, что уравнению, точно так же как и выражению, можно присвоить имя. В следующей командной строке мы введём уравнение и присвоим ему имя " eq1 " :

> eq1:=x^3-5*x^2+23=2*x^2+4*x-8;

Мы можем вывести на экран левую и правую части уравнения по-отдельности при помощи команд lhs и rhs :

> lhs(eq1);

> rhs(eq1);

Воспользуемся командами lhs и rhs для того, чтобы привести уравнение к стандартному виду, в котором все члены собраны слева, а справа остался только 0:

> eq2:=lhs(eq1)-rhs(eq1)=0;

04. 02 Нахождение точных корней. Команда solve

* Finding Exact Solutions: The solve command *

Рассмотрим вначале рациональные уравнения. Известно, что существуют алгоритмы определения точных корней рациональных корней вплоть до 4-го порядка включительно. В Maple-команду solve и заложены эти алгоритмы.

Воспользуемся командой solve для нахождения точных корней кубического уравнения :

> solve(3*x^3-4*x^2-43*x+84=0,x);

Обратите внимание: в команде мы указываем, относительно какой переменной следует решать уравнение. Хотя в нашем конкретном случае это и не обязательно:

> solve(3*x^3-4*x^2-43*x+84=0);

Maple нашел все 3 действительных корня и вывел их (в неупорядоченном виде ).

Иногда очень важно выбрать конкретный корень, чтобы потом использовать в дальнейших преобразованиях именно его. Для этого заранее следует присвоить имя результату исполнения команды solve . Назовём его X . Тогда конструкция X будет соответствовать первому корню из списка (подчеркнем: это не обязательно меньший корень! ), X - второму корню, и т.д. (Скобки - квадратные! ):

> X:=solve(x^2-5*x+3=0,x);

Посмотрите, однако, что будет выведено в результате выполнения похожей команды:

> x=%;

Ещё раз подчеркнём: практика показывает, что уравнению целесообразно присвоить имя. Традиционно в Maple такое имя начинается с букв eq :

> eq1:=7*x^3-11*x^2-27*x-9=0;

(Не путать оператор присваивания " := " со знаком равенства " = " !)

Теперь решим уравнение при помощи команды solve . Множеству корней присвоим имя X :

> X:=solve(eq1,x);

Для убедительности проверим, нет ли среди найденных корней посторонних. Проверку выполним непосредственной подстановкой

> subs(x=X,eq1);

Разумеется, частенько "точные" решения довольно громоздки, если не сказать иначе. Например, это касается уравнения :

> eq1:=x^3-34*x^2+4=0;

> X:=solve(eq1,x);

Теперь Вам понятно, о чем речь? Для себя заметьте, что мнимая единица в Maple обозначается посредством прописной буквы I . Разумеется, в таких случаях не грех найти приближенные значения корней. Имея на руках точное решение, Вы и сами сообразите, как это сделать:

> evalf(X);

В подобных ситуациях хорошей альтернативой команде solve является fsolve , особенности которой будут рассмотрены в следующем параграфе.

Команда solve используется при отыскании точных решений не только рациональных уравнений. Ниже приведено несколько тому иллюстраций. Но для многих типов иррациональных, показательных, логарифмических, тригонометрических и даже рациональных уравнений точное решение искать бесполезно. На помощь призывается команда fsolve .

Решим уравнение :

> solve(5*exp(x/4)=43,x);

Иногда (а в тригонометрии - всегда ) Maple, по умолчанию , не выводит всё множество корней:

> solve(sin(x)=1/2,x);

Но безвыходных ситуаций не бывает! Взяв за основу полученный результат, воспользуйтесь своими знаниями тригонометрических уравнений и запишите полное решение (как? ).

Упражнение 4.1

Решить уравнение Разберитесь, сколько различных корней имеет уравнение. Как Maple поступает при наличии равных корней?

Совет : разложите на множители левую часть уравнения.

> solve(x^3-11*x^2+7*x+147=0,x);

> factor(x^3-11*x^2+7*x+147);

Корень х = 7 является двукратным, а потому у кубического уравнения только два различных корня. Разложение на множители левой части уравнения - тому подтверждение.

04. 03 Поиск приближенных корней. Команда fsolve

* Finding Approximate Solutions: The fsolve command *

Для приближенного решения уравнений используется Maple-команда fsolve . В случае рационального уравнения, fsolve выводит весь список действительных корней (см. Пример 01). Для трансцендентных уравнений эта команда, по умолчанию, выводит только один корень (см. Примеры 02 и 03).

При помощи fsolve найдём приближенные значения сразу всех четырёх действительных корней рационального уравнения :

> eq:=x^4-x^3-17*x^2-6*x+2=0;

> fsolve(eq,x);

Эти четыре корня и составляют исчерпывающее решение исходного рационального уравнения (хотя и приближенное ).

Используя команду fsolve , найти хотя бы один действительный корень уравнения :

> eq:=x^3+1-exp(x)=0;

> fsolve(eq,x);

Maple и вывел только один корень. На этот раз Maple не стал "живописать". Как теперь убедиться в том, что других действительных корней нет? Следующий пример даёт такой инструментарий.

Получить все действительные корни уравнения и убедиться в этом.

Шаг первый ( Основная идея ) : найдём графическое решение уравнения. Для этого построим график функции, стоящей в левой части уравнения. Абсциссы точек пересечения этого графика с осью Ох и будут искомыми корнями.

> plot(x^3+1-exp(x),x=-3..5,y=-5..15);

Т.к. мы умело подобрали диапазоны изменений абсцисс и ординат точек графика, то легко обнаружим 4 точки пересечения линии с осью Ох. Одна из них соответствует корню, найденному в Примере 02 (какая именно? ).

Второй корень очевиден: х = 0. А как поточнее найти остальные?

Шаг второй ( Уточнение ) : применим команду fsolve более "зряче". В Maple предусмотрена возможность указания промежутка, на котором отыскиваются корни. В частности, для определения отрицательного корня нашего уравнения, укажем, что поиски следует вести в "районе" [-1;-0.2]. Об этом красноречиво свидетельствует графическое решение.

> fsolve(eq,x=-1..-.2);

Оставшиеся корни явно принадлежат промежуткам и . Расскажем об этом команде fsolve :

> fsolve(eq,x=1..2);
fsolve(eq,x=4..5);

Ну а что произойдёт, если мы подсунем Maple "пустой участок"? Например, отрезок для нашего уравнения. Там графического решения явно нет:

> fsolve(eq,x=2..4);

Maple выдаёт название команды, само уравнение, имя аргумента и отрезок. Т.е. ничего нового. Мол: "Ищите корни сами, а я не нашел".

Шаг третий ( Дополнительный анализ ) : Как теперь удостовериться в том, что найдены все корни , а не только в видимой области графического решения? Для этого следует расширить интервал поисков:

> plot(x^3+1-exp(x),x=-3..50,y=-10..15);

Новых точек пересечения нет. В конце концов мы понимаем, что экспоненциальное слагаемое на границах промежутка вносит самый существенный вклад в величину функции из левой части уравнения. Значения функции в этой области стремятся к , а потому дополнительных корней нам не найти.

Попробуем в других местах: справа и слева от области найденных корней.

> fsolve(eq,x=5..50);

> fsolve(eq,x=-50..-1);

И здесь ни одного дополнительного корня! Поняв, что с влиянием показательной части уравнения всё ясно, делаем окончательные выводы.

Исчерпывающее решение уравнения состоит из четырёх корней: -.8251554597 , 0 , 1.545007279 , 4.567036837 .

Применим команду fsolve для приближенного решения трансцендентного уравнения .

Как и в предыдущем случае, найдём вначале качественное графическое решение. Для этого ещё нужно угадать, как разбросать по обеим частям уравнения его члены. Но графические возможности Maple настолько великолепны, что почти всегда можно собирать все члены уравнения с одной стороны.

Рассмотрим уравнение, равносильное данному: . Абсциссы точек пересечения графика функции, стоящей в левой части уравнения, с осью Ох и будут искомыми корнями.

> eq:=x^2/20-10*x-15*cos(x+15)=0;

> plot(lhs(eq),x=-10..10);

График указывает область поисков корней: промежуток . Настаёт черёд команды fsolve :

> fsolve(eq,x=1..2);

Корень найден. Но, очевидно, он - не единственный. Расширьте область поисков и ещё раз примените команду fsolve для отыскания второго корня.

Упражнение 4.2

Найти все действительные корни уравнения , начав с графического решения.

Построим график левой части уравнения:

> eq:=x^5-4*x^3+3*x^2+7*x-1=0;

> plot(lhs(eq),x=-5..5,y=-5..5);

В результате находим корни уравнения в первом приближении: -2 ; -1.5 ; 0 . Применим теперь команду fsolve без указания диапазона поиска (оценим возможности Maple ):

> fsolve(eq,x);

С удовлетворением отмечаем, что Maple выводит все три корня (Не будем забывать, что решали рациональное уравнение.)

Упражнение 4.3

Найти все корни уравнения . Воспользуйтесь графическим решением. Проверьте каждый корень непосредственной подстановкой.

Приведём уравнение к стандартному (для этого раздела) виду:

> eq:=x^2-2-ln(x+5)=0;

Теперь построим график левой части уравнения:

> plot(lhs(eq),x=-10..10);

По всей видимости, существует два корня. Один примерно равен -2, а другой, похоже, 2.

Применим команду fsolve , ограничив диапазон поиска:

> x:=fsolve(eq,x=-5..0);

> x:=fsolve(eq,x=1..3);

Непосредственной подстановкой проверим корни:

> evalf(subs(x=x,eq));

Обратите внимание: в обоих случаях истинного равенства нет. С учётом ошибок при округлении, разумное расхождение вполне допустимо.

Убедитесь в отсутствии других корней. Ответ обоснуйте.

Упражнение 4.4

Графики функций и дважды пересекаются на отрезке [-5;5].

а). Постройте в одной системе координат графики обеих функций и при помощи мыши найдите координаты точек пересечения.

b). Составьте уравнение, корнями которого являются абсциссы точек пересечения графиков.

c). Используйте команду fsolve для решения этого уравнения.

d). Используйте результаты из пункта с) для оценки ординат точек пересечения графиков.

e). У Вас не создалось впечатление, что линии могут пересекаться и в третьей точке с координатами (1;9)? Используйте fsolve и графические возможности Maple, чтобы убедиться в противном.

> y1:=10-x^2;

> y2:=4*sin(2*x)+5;

Теперь построим графики функций:

> plot(,x=-5..5);

Приближенные координаты точек пересечения: (-1.8, 6.6) и (2.75, 2) .

b) Составим уравнение:

> eq:= y1=y2;

с) Команда fsolve поможет найти соответствующие корни:

> x1:=fsolve(y1=y2,x=-4..0);

> x2:=fsolve(y1=y2,x=0..4);

d) Используем команду subs для определения соответствующих ординат точек пересечения:

> y:=subs(x=x1,y1);

> y:=subs(x=x2,y1);

Общие точки графиков: (-1.800,6.763) и (2.773,2.311) .

e) Графически исследуем окрестность точки х = 1:

> plot(,x=.5..1.5);

Команда fsolve на этот раз позволит доказать отсутствие корней вблизи точки х = 1:

> fsolve(y1=y2,x=.5..1.5);

04. 04 Решение уравнений в общем виде

* Solving Literal Equations *

Во многих случаях Maple находит решение уравнения в общем (символьном) виде. Речь идёт об уравнении (а не системы!), содержащем несколько переменных. Решение состоит в том, что какая-то из переменных выражается через остальные.

Пусть необходимо решить уравнение относительно переменной g . По привычке, используем команду solve . И она оправдывает наши надежды: